Excellent Partition Magic for Win 7 – MiniTool Partition Wizard

The Popularity of Windows 7

Are you a Windows 7 user? How do you think of it? According to netmarketshare, Windows 7 holds the first place of desktop operating system market share, with an overwhelming proportion that reaches up to 49.42% (March 2017). This demonstrates that Windows 7 is still the most popular operating system around desktop users world-wide, despite that Microsoft is aggressively pushing Windows 10 . Since so many users are choosing Windows 7, it is important to have professional partition magic for Windows 7 so that users can manage their hard drives better.

“Anyone recommend some free software that a newbie can use to make partitions? I’ve tried SwissKnife but it won’t let me use any of the basic commands (the create button won’t let me press it, and the slider for choosing space allocation won’t let me change it). And all other software I’ve tried is Demo version only, meaning it doesn’t do ****.
So, can anyone recommend a program? Time limited shareware would be fine if it let me make a partition or two before the duration ran out. Thanks!” –from Tomsguide

And in today’s post, what we are going to introduce is two pieces of partition manager software.

Built-in Partition Manager for Windows 7 – Disk Management

Disk Management is an extension of the Microsoft Management Console that allows users to fully manage the disk-based hardware recognized by Windows, like hard disk drives (both internal and external ones), flash drives and optical disk drives. Disk Management can be used to partition drives, format drives, extend volumes, shrink volumes, convert dynamic disk to basic, and much more. By clicking a drive or a disk, users clearly know what Disk Management can do to it.

Here is the full list of Disk Management features:

See Disk Management is really a useful tool that can satisfy most of our needs on disk partition management. However, sometimes due to some limitations, some features get inactivated. For example, while trying to expand storage space of a volume, “Extend Volume” feature greyed out. Besides, many features should be carried out on condition that all partitions are deleted or the hard drive is formatted, bringing much inconvenience to us.

Professional Partition Manager Windows 7 – MiniTool Partition Wizard

MiniTool Partition Wizard is an outstanding partition magic for Windows 7 which runs perfectly under 32/64bit operating systems like Windows XP, Windows Vista, Windows 7/8.1/10 as well as Windows Server 2003/2008/2012 and Windows Server 2016. As is known to us, managing partition under Windows operating system is a tough task since the system built-in Disk Management tool doesn’t offer enough functions to meet the increasing user demands.

Therefore, we can turn to third-party partition magic software to realize those operations such as merge partition, copy partition, convert FAT to NTFS without formatting, convert MBR GPT without deleting partition, convert dynamic disk to basic disk, etc. As we have recommended, MiniTool Partition Wizard is such an outstanding partition magic for Windows 7. Not only does it offer almost all features listed on the table, but also provide more than we can see from the table.

MiniTool Partition Wizard FreeClick to Download100%Clean & Safe

MiniTool Partition Wizard has the following advantages over Windows Disk Management:

Compared with Windows built-in Disk Management utility, MiniTool Partition Wizard helps to solve disk partition issues flexibly and safely. To be more specific, we would like to do some comparisons.

1. Extend Partition

While using Disk Management to extend a partition, some unallocated space/free space are needed. Besides, the unallocated space/free space should be continuously following the target partition. Hence, Disk Management always fails to do an extension.

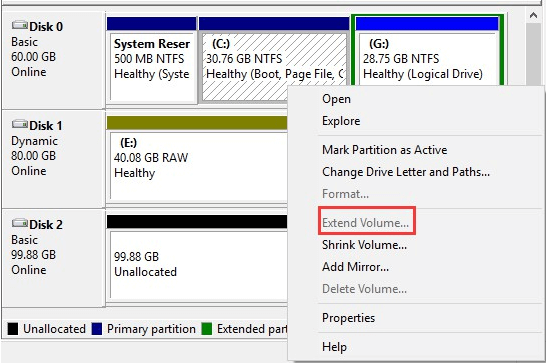
However, in MiniTool Partition Wizard, things are much different. Only 3 steps we can extend a partition even though there is no unallocated space/free space offered on the same drive.

Step 1. On the main interface, select the partition we want to extend and choose “Extend Partition” from the action panel.

Step 2. In the pop-up new window, choose a partition to take some free space from and then slide the slider to determine how much free space is needed.

Step 3. Click “Apply” button to save this change.

See! This partition magic for Windows 7 is really flexible. But this is not all. In fact, it can do a lot of other things flexibly, just keep reading.

2. Convert Disk to MBR/GPT

While most time we use MBR partition style, sometimes we need to convert MBR disks to GPT disks. For example, to make full use of disk space of hard drives larger than 2TB, we need to convert MBR disk to GPT disk. However, using Disk Management requires deleting all partitions on it before we can make the conversion.

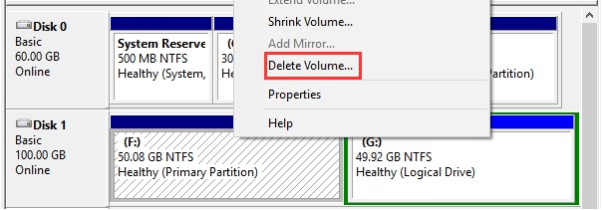
What if we use partition software for Windows 7 – MiniTool Partition Wizard?

Let’s take a look at the operations:

Step 1. After running this partition software for Windows 7, select the disk we need to convert (here is Disk 2) and then choose “Convert MBR Disk to GPT Disk” from the action panel.

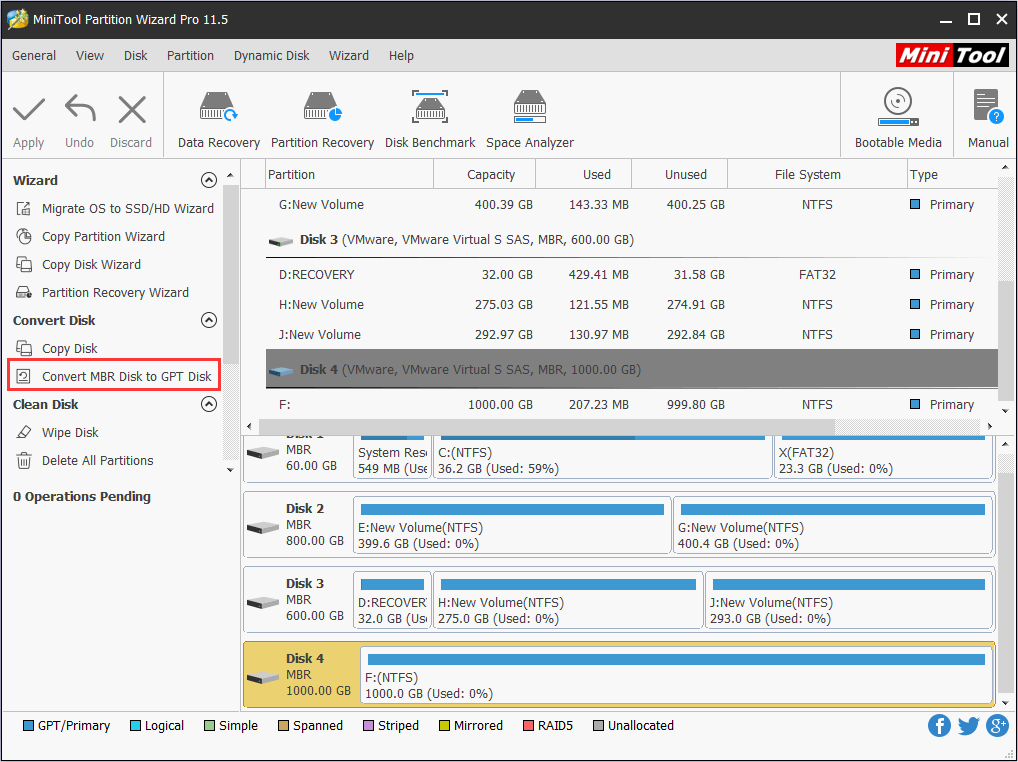
Step 2. See! Without deleting any partition, we can successfully convert the MBR disk to GPT disk. What if we want to revert the disk to MBR some day? Well, the feature “Convert GPT Disk to MBR Disk” will help you to complete this task.

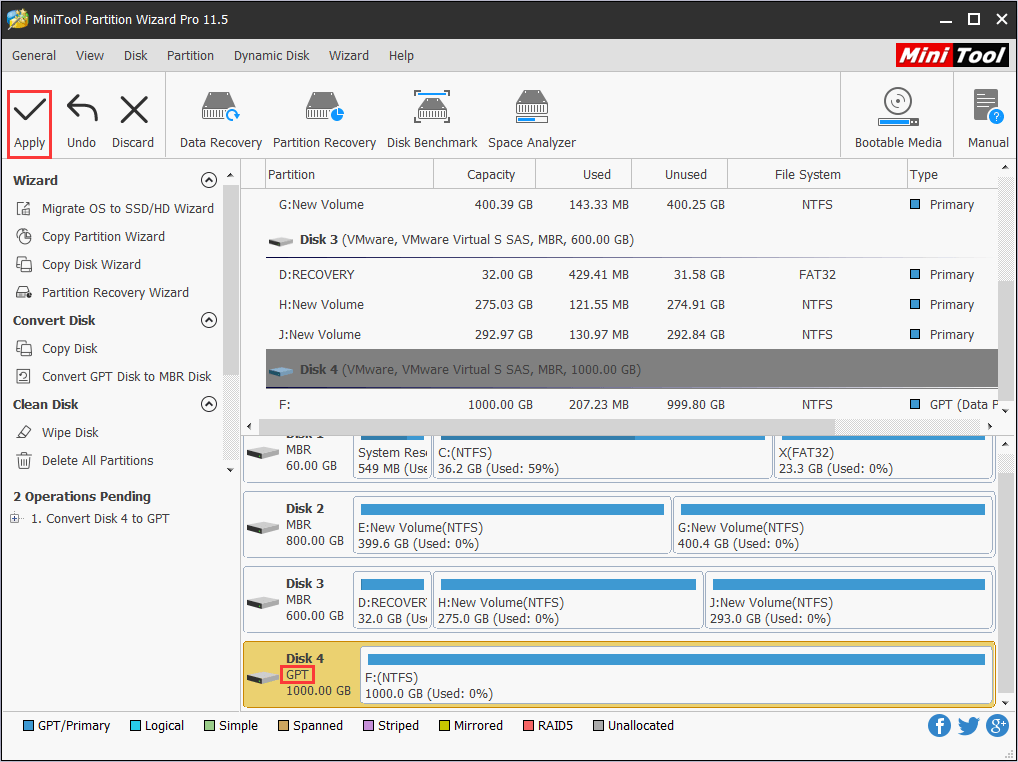
3. Convert File System

The next aspect we want to show you is MiniTool Partition Wizard works excellently in converting file systems. Today, NTFS is the most popular file system that has been widely used on hard drives, SSDs, external hard drives and USB flash drives. However, while connecting the storage device to computers running old operating systems or some play stations, FAT 32 is still the choice. So we need to convert NTFS partition to FAT 32 partition.

Can we do this job using Windows Disk Management? Of course! But the choices are either to format the partition to FAT 32 or delete that partition first and then recreate partition using FAT 32 file system.

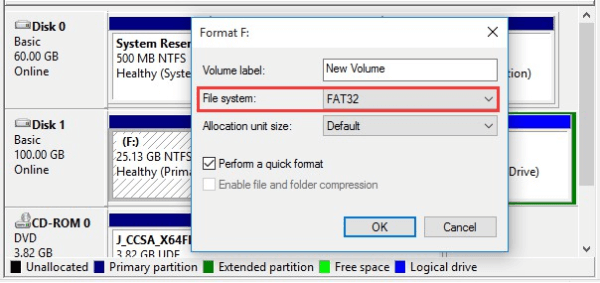
Now let’s see how MiniTool Partition Wizard performs towards this issue:

Step 1. On the main interface of MiniTool Partition Wizard, select the partition that should be converted to FAT 32 and then choose “Convert NTFS to FAT” from the action panel.

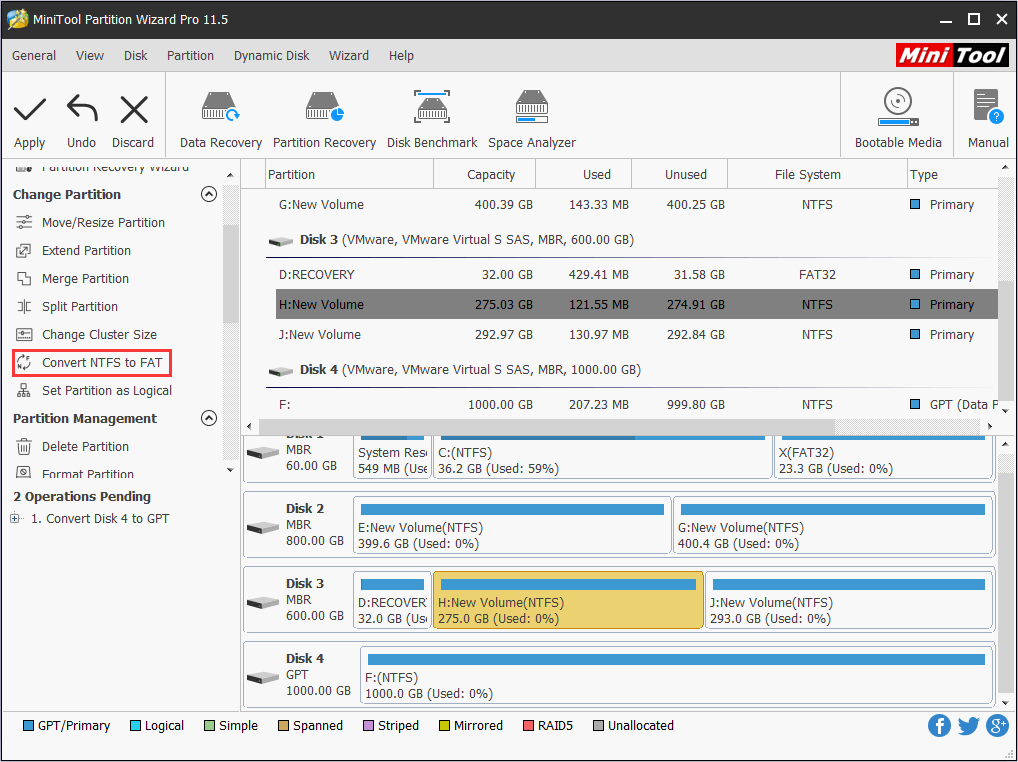
Step 2. We can see the file system will be turned into FAT 32. Now hit “Apply” to confirm this change.

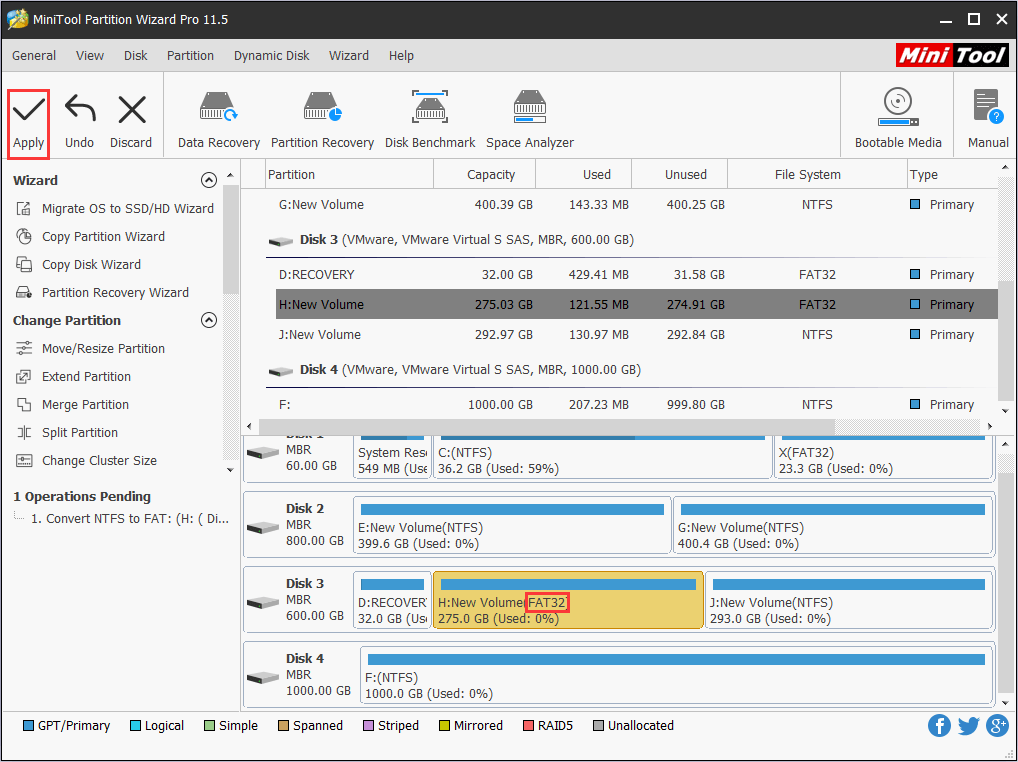
As we can see from the above picture, MiniTool Partition Wizard not only can convert NTFS partition to FAT32 directly without damaging data but also breaks the limit of the 32 GB partition size limit. What’s more, it can convert FAT 32 to NTFS whenever we want. Hence, we say it is flexible partition manager Windows 7.

Click to Tweet

4. Convert Dynamic Disk to Basic

While most of the time, we use basic disk as the storage type, sometimes we may find that the drive has turned to dynamic disk accidentally. To know why hard disk becomes dynamic disk, check 3 Situations Where Hard Disk Will Become Dynamic. In this case, we may find that dynamic disk is not as easy to manage as a basic disk, hence we want to convert dynamic disk to basic disk.

Then how can we revert a dynamic disk to basic disk?

In Windows 10 Disk Management, delete all volumes on the dynamic disk and then the dynamic disk is converted to basic disk automatically. (In some earlier OS, we still need to select the dynamic disk and then choose “Convert to Basic Disk”)

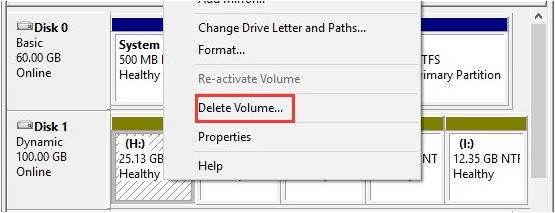
What if all volumes are of great significance to us? Well, if we want to avoid the process of making volume backup, we had better turn to MiniTool Partition Wizard for help, which is able to convert dynamic disk to basic disk without bringing any data loss.

Step 1. Launch this partition software for Windows 7, then select the dynamic disk that needs converting and choose “Convert Dynamic Disk to Basic Disk” from action panel.

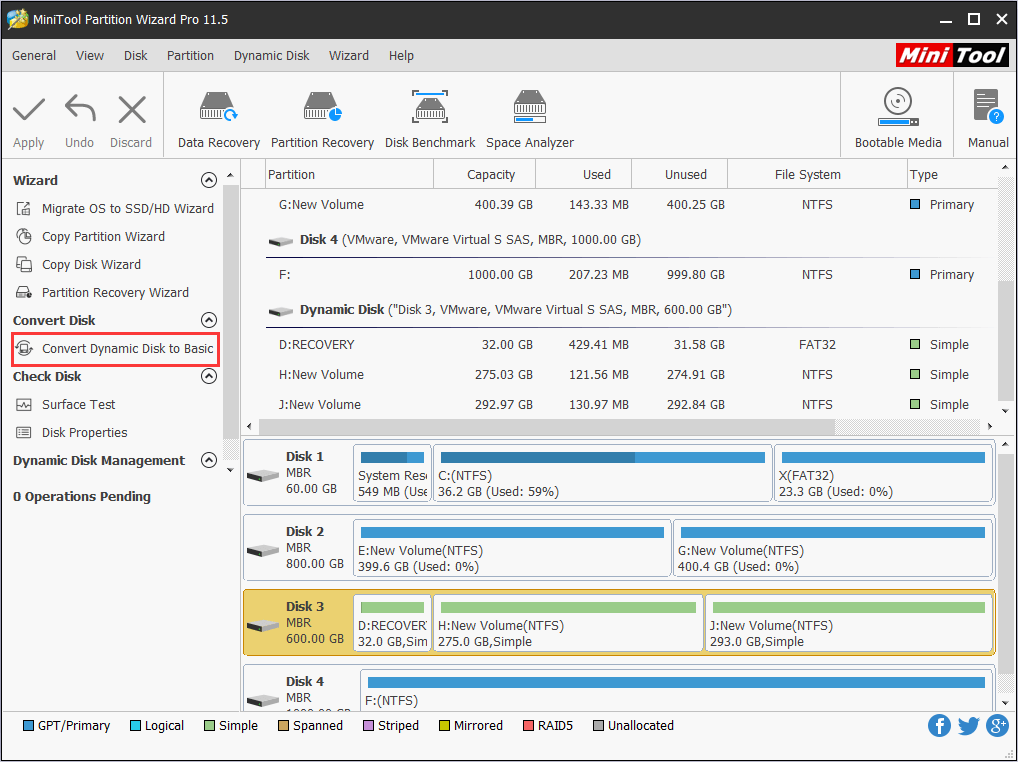
Step 2. We can see from the sample picture that all simple volumes will turn to primary partitions and logical partitions on basic disk. Now we can press “Apply” from the tool bar to confirm this conversion.

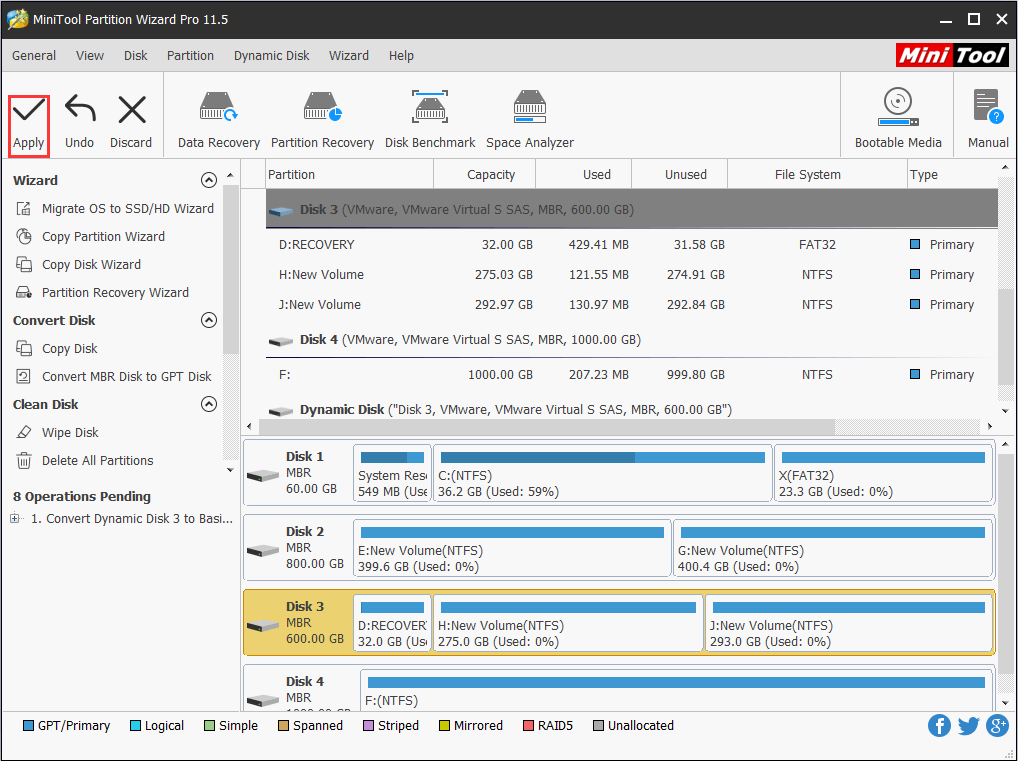
5. Migrate OS & Copy Disk

And one of the most widely used features MiniTool Partition Wizard offers (Disk Management lacks) is “Migrate OS to SSD/HD”, which helps to copy the current OS to another hard drive. This is a totally safe and beneficial feature and does no harm to the original OS disk. Once we have the requirement to migrate OS to faster SSD or a larger hard drive, we can use this feature.

Step 1. After launching partition magic for Windows 7, select “Migrate OS to SSD/HD” from the tool bar.

Step 2. Immediately we can see a page which enables to choose whether to migrate the OS only or to copy the whole drive. Here we just take the copy all partitions for example. Then click “Next” to continue.

Step 3. Here we need to select a destination disk which should be a basic disk and should be large enough to contain all contents on the source disk. Be aware that all data on the selected disk will be removed. Then click “Next” to go on.

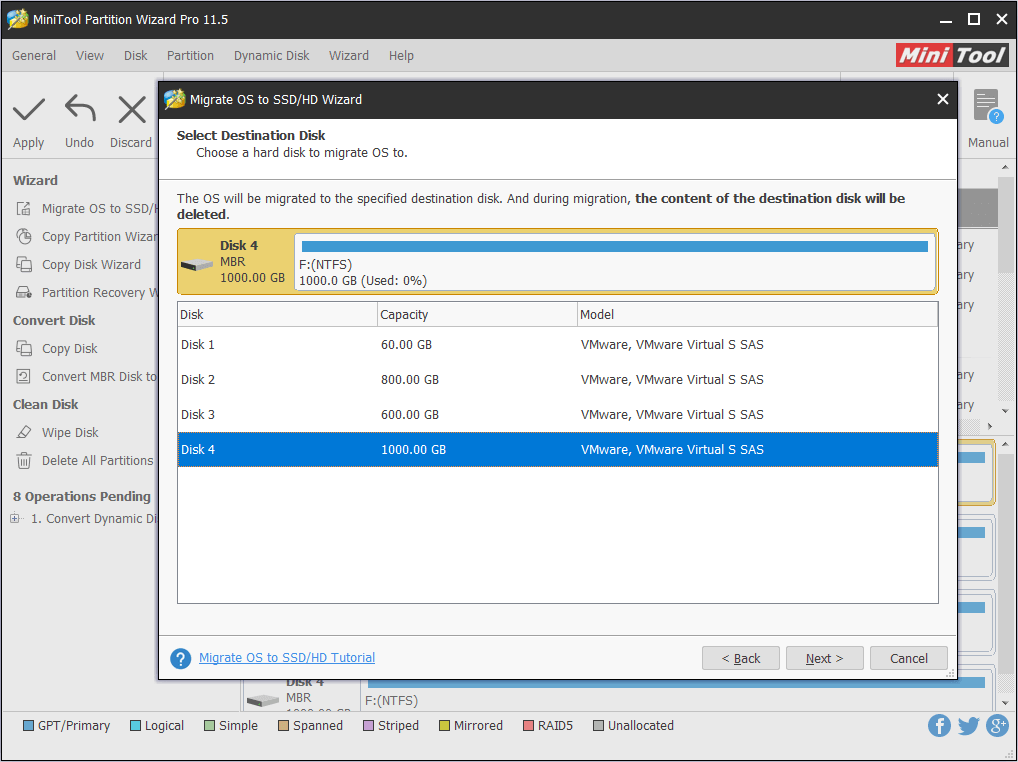
Step 4. Now four options are provided here. We can choose to fit partitions to entire disk or to keep the original partition size proportion when the target disk is not smaller than the original one. Besides, we can select “Align partitions to 1MB” and “Use GUID Partition Table for the target disk“. After the selection, click “Next” to continue.

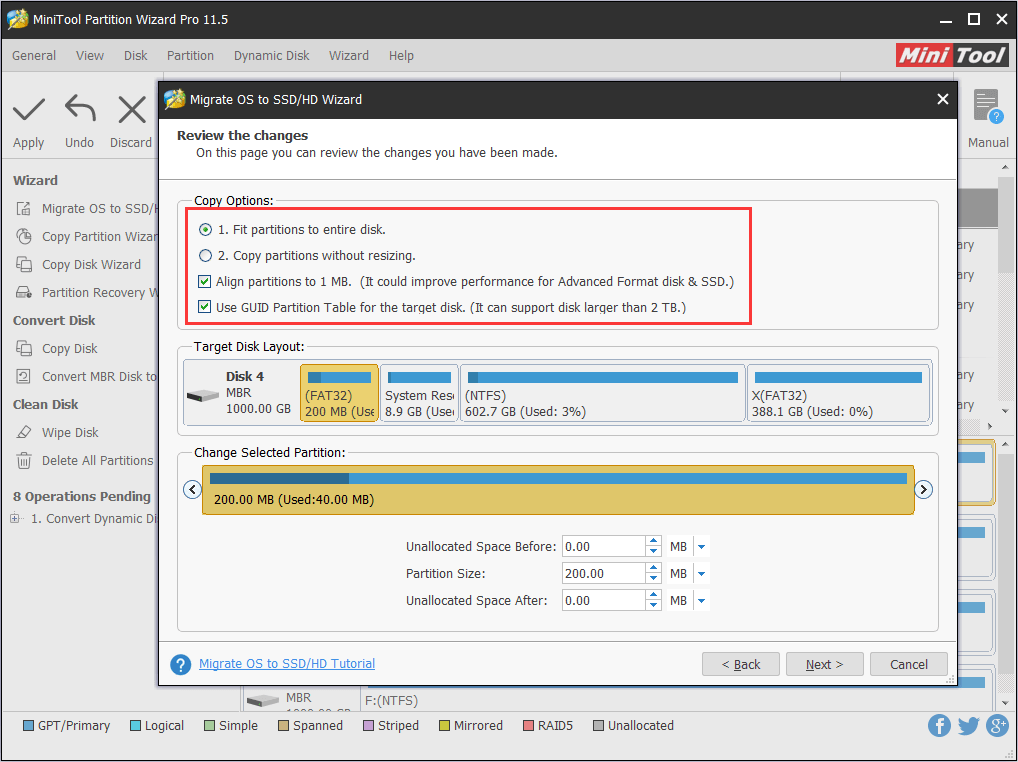
Step 5. MiniTool Partition Wizard will tell us how to boot from the target disk. We should pay attention to the message before clicking “Finish“.

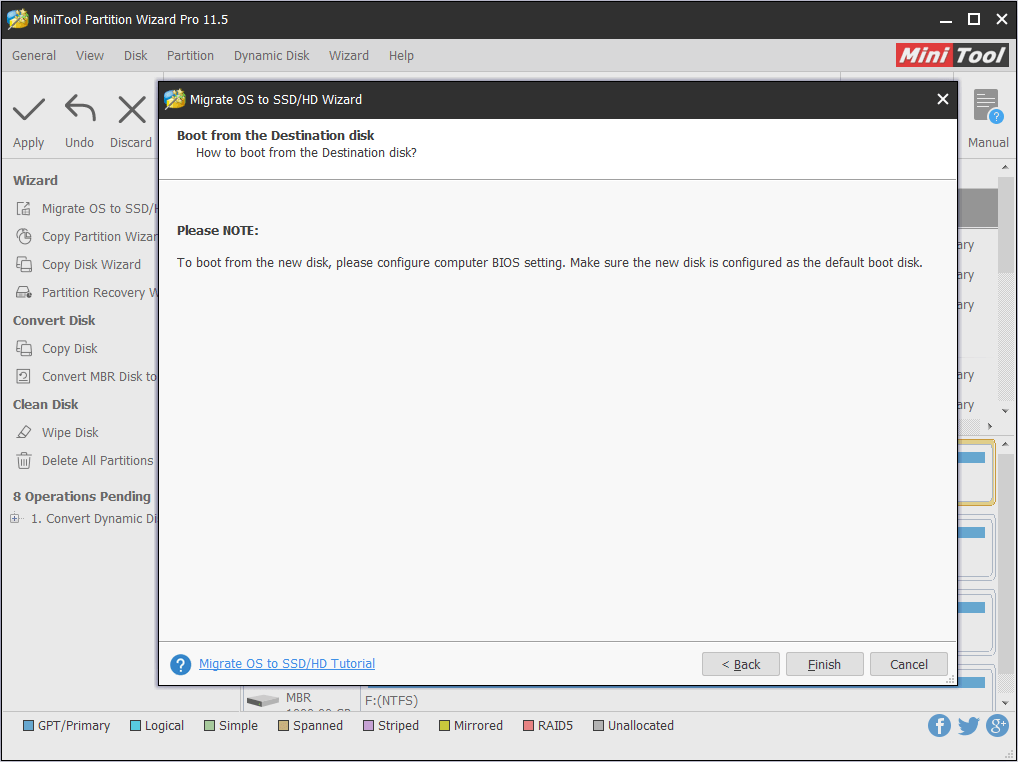
Step 6. Finally, click “Apply” to start the system migration after we confirm what is going to happen.

6. Create Bootable Media

The most outstanding feature, we think, is that MiniTool Partition Wizard offers Bootable Media Builder to create bootable Partition Wizard to manage hard drives when Windows fails to boot (also not provided by Disk Management). This tool is very important because “Missing Operating System“, “Boot Device Not Found”, “BOOTMGR Is Missing” etc. can happen without any omen. But as long as we have MiniTool Partition Wizard and have created a bootable rescue media in advance, and then use it to try to fix such issues.

The End

After seeing the above comparisons between MiniTool Partition Wizard and Windows built-in Disk Management utility, we can draw a conclusion that MiniTool Partition Wizard offers more flexible ways to manage hard disks and partitions, in a safe and more user-friendly way. So next time when we have the requirement of Windows 7 disk management, we can turn to this hard drive partition software to get the full and powerful features.

Are you still looking for the best partition magic for Windows 7? Get MiniTool Partition Wizard right now. Should you have any questions while using this Windows 7 partition manager, you can leave us comments below or send us an email via [email protected]